单片机的二进制与十六进制芯片解密
芯片解密二进制(binary),是在数学和数字电路中以2为基数的记数系统,是以2为基数代表系统的二进位制。这一系统中,通常用两个不同的符号0(代表零)和1(代表一)来表示。发现者是莱布尼茨。数字电子电路中,逻辑门的实现直接应用了二进制,现代的计算机和依赖计算机的设备里都使用二进制。每个数字称为一个比特(Bit,Binary digit的缩写)。
数字电路中只有两种电平特性,即高电平和低电平,这也就决定了数字电路中使用二进制。十进制数大家应该都不陌生,“逢十进一,借一当十”是十进制数的特点。有了十进制数的基础,我们学习二进制数便非常容易了,“逢二进一,借一当二”便是二进制数的特点。
十进制转换为二进制
一个十进制数转换为二进制数要分整数部分和小数部分分别转换,最后再组合到一起。
整数部分采用"除2取余,逆序排列"法。具体做法是:用2整除十进制整数,可以得到一个商和余数;再用2去除商,又会得到一个商和余数,如此进行,直到商为小于1时为止,然后把先得到的余数作为二进制数的低位有效位,后得到的余数作为二进制数的高位有效位,依次排列起来。
芯片解密十进制数1转换为二进制数是1B(这里B是表示二进制数的后缀);十进制数2转换为二进制数时,因为已经到2,所以需要进1,那么二进制数即为10B;十进制数5转换为二进制数,2为10B,那么3即为10B+1B=11B,4即为11B+1B=100B,5即为100B+1B=101B。依次类推,当十进制数为254时,对应二进制数为11111110B
我们可找出一般规律,当二进制数转换成十进制数时,从二进制数的最后一位起往前看,每一位代表的数为2的n次幕,这里的n表示从最后起的第几位二进制数,n从0算起,若对应该二进制数位上有1,那么就表示有值,为0即无值。例如,再把二进制数11111110B反推回十进制数,计算过程如下:
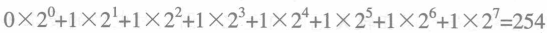



 芯片解密
芯片解密